Understanding Bubble Sort: More Than Just Code

Introduction

Hey guys, welcome to my blog! This is actually my first post in the problem-solving series. In this post, we’re going to look at a sorting algorithm called Bubble Sort.

Now wait — I know you’ve already seen bubble sort in many tutorials.

But here, I want to share it in a different way:

• How to think about the logic
• How it works step by step
• How to optimize the code
• Why do we do that?
• How to understand it mathematically

Before diving into bubble sort, there’s something important.

We need to understand computer science.

Computer science is the study of information – how it’s represented and how it’s computed.

Why are we learning bubble sort and all these basic algorithms?

Because bubble sort is one of the fundamental algorithms in computer science.

So, What is an Algorithm?

An algorithm is a very precise set of instructions designed to solve a computational problem. It takes a set of inputs to produce a set of outputs within a finite amount of time.

And algorithms aren’t just for computers. We actually use algorithms in our daily lives, too.

Daily Life Analogy of Algorithms

For example: How do you brush your teeth?

• Walk to the bathroom
• Take the brush and rinse it in the sink
• Apply the toothpaste and brush your teeth

Precise vs Vague Instructions

But if you notice, these steps are vague. I haven’t given precise instructions because you use your common sense, but computers don’t.

Computers are literally dumb. They need not only precise, but very accurate instructions.

If you don’t give the exact steps, the program crashes.

How does a precise algorithm look?

For example: How do you teach your computer to brush your teeth?

• Wake up from bed
• Walk a few steps to reach the bathroom
• Take the toothbrush and toothpaste from the left corner shelf
• Rinse the brush in the sink
• Apply the toothpaste to the brush
• Close your toothpaste
• Brush your teeth:
  • Upper teeth 4 times
  • Lower teeth 4 times, etc.
• Rinse your mouth with water
• Rinse toothbrush
• Return the toothbrush and toothpaste to the shelf
• Done

So this precise algorithm looks like this.

But even here, I’ve left out a few important steps.

What if you didn’t close the bathroom door?

Someone might walk in and interrupt you – that’s an unexpected behavior.

In programming, we call that a bug – when your program doesn’t handle a certain situation correctly and ends up doing something wrong or even crashing.

Why am I saying all this to you?

Because you need to think, not just memorize.

Don’t just blindly cram bubble sort for a random tech interview. Instead, understand what it actually is—how it works, why it matters, and what it teaches you about problem-solving.

What is Bubble Sort?

Bubble Sort is a simple sorting algorithm that compares pairs of adjacent elements and swaps them if they are in the wrong order. This process is repeated until the array is sorted either in increasing or decreasing order.

Bubble Sort Analogy

Imagine in school, the students are standing in a prayer line or for a class photo. The teacher wants to arrange the students in order based on height. If someone is shorter, they go in front. If someone is the tallest, they go to the back.

This is repeated until the shortest student goes forward and the tallest student goes backward.

In each round, the tallest student “bubbles up” to the end like a bubble rising to the surface in water.

How does it work?

1. Take the unsorted data from the user, for example: {6, 4, 5, 3, 2, 1}
2. Compare pairs of adjacent elements; if the first is larger than the second, swap them. i.e., if a_j > a_j+1, then swap a_j and a_j+1.
3. Repeat until the array is sorted.

It looks simple, right? Let’s briefly explain how bubble sort works.

First, take the unsorted data: {6, 4, 5, 3, 2, 1}. To sort this list using bubble sort, we need to compare and swap the elements repeatedly until the entire list is in order.

Do we need to use loops?

In this case, we use two loops: one is the outer loop and the other is the inner loop.

The outer loop iterates over the elements multiple times, while the inner loop performs the comparisons.

Why are we using two loops?

Because we need to compare each and every element. If we use a single loop, only one element gets sorted; the others do not.

Let’s start with iteration. In the first iteration, where i = 0 and i < n, we start comparing elements from the beginning.

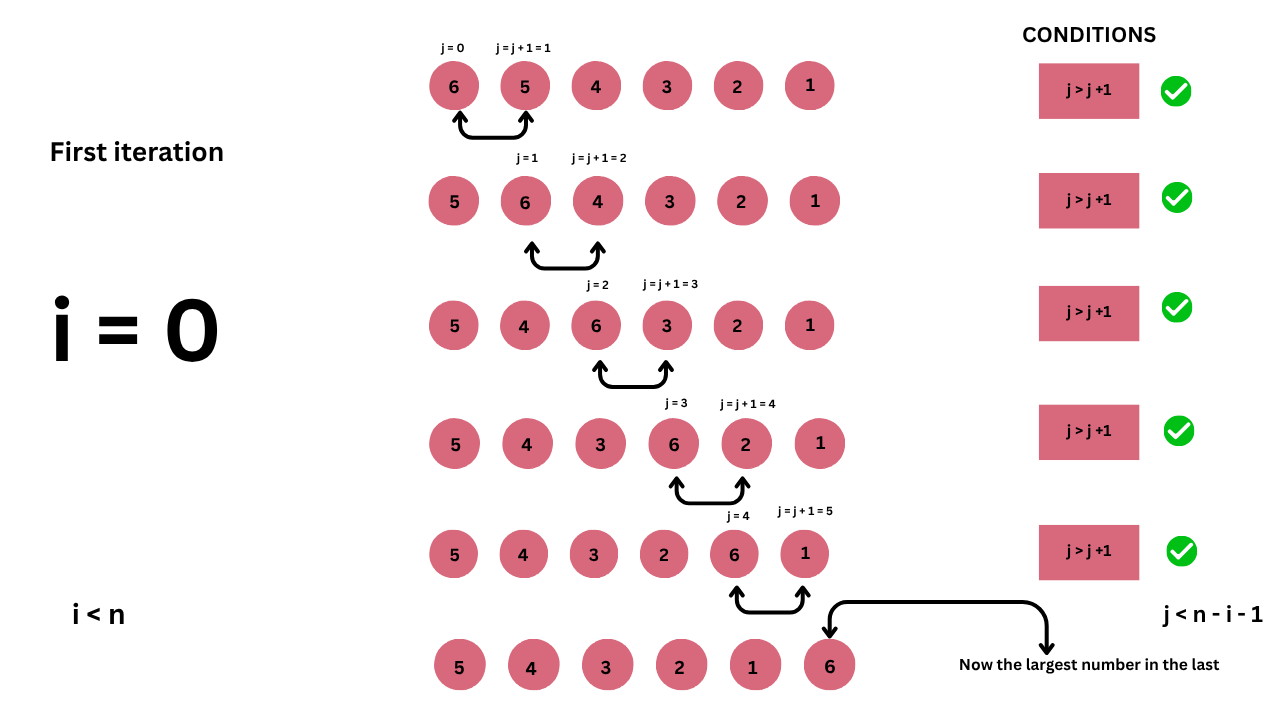
Let’s go through the first pass of bubble sort step by step using the list:

We start with i = 0 (first iteration), and we’ll compare each pair of neighboring elements using an inner loop.

You may be wondering what j and j + 1 are. Basically, j represents the current element, and j + 1 is the neighboring element that it’s being compared with.

1. Compare 6 and 5
   • Since 6 is greater than 5, swap the elements.
2. Compare 6 and 4
   • Since 6 is greater than 4, swap the elements.
3. Compare 6 and 3
   • Since 6 is greater than 3, swap the elements.
4. Compare 6 and 2
   • Since 6 is greater than 2, swap the elements.
5. Compare 6 and 1
   • Since 6 is greater than 1, swap the elements.

Now you can clearly see that the largest element moves towards the end, just like a bubble rising to the surface (when you boil water). That’s why it’s called bubble sort.

Next, we move to the second iteration, i = 1.

In the second iteration, we take the list {5, 4, 3, 2, 1, 6}, which is the result after the first iteration.

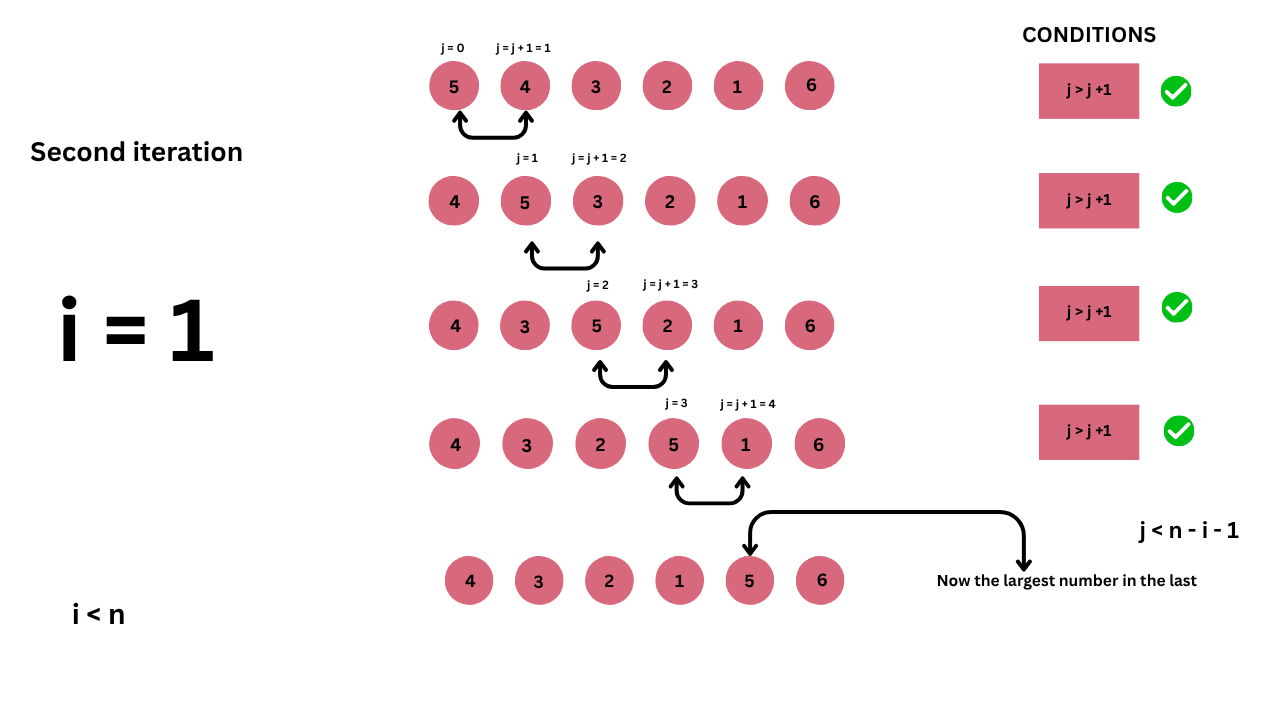
Here, you can clearly see that the last number is the largest. So, in every iteration, the biggest number goes to the last.

Let’s start the second iteration.

1. Compare 5 and 4
   • Since 5 is greater than 4, swap the elements.
2. Compare 5 and 3
   • Since 5 is greater than 3, swap the elements.
3. Compare 5 and 2
   • Since 5 is greater than 2, swap the elements.
4. Compare 5 and 1
   • Since 5 is greater than 1, swap the elements.

In this case, we don’t compare 5 and 6 because 6 is already in its correct (sorted) position.

To avoid comparing with elements that are already sorted at the end of the list, we use the condition j < n - i - 1 in the inner loop.

This condition ensures that with each iteration of the outer loop (i), we reduce the number of comparisons, since the largest elements have already “bubbled up” to the end.

For example:

• In the first iteration, i = 0 so the condition becomes j < n - 1.
• In the second iteration, i = 1, so the condition becomes j < n - 2.

In a nutshell, this condition helps to avoid unnecessary comparisons with elements that are already sorted at the end of the list. With each pass, the biggest number settles in place, so the inner loop doesn’t need to check those again.

For example: {5, 4, 3, 2, 1, 6}, where n = 6;

So n - 2 = 4, meaning the inner loop only checks up to index 4 and doesn’t compare with the already sorted 6 at the end.

This is a simple form of optimization in bubble sort.

In the third iteration, we take the list {4, 3, 2, 1, 5, 6}, which is the result after the second iteration.

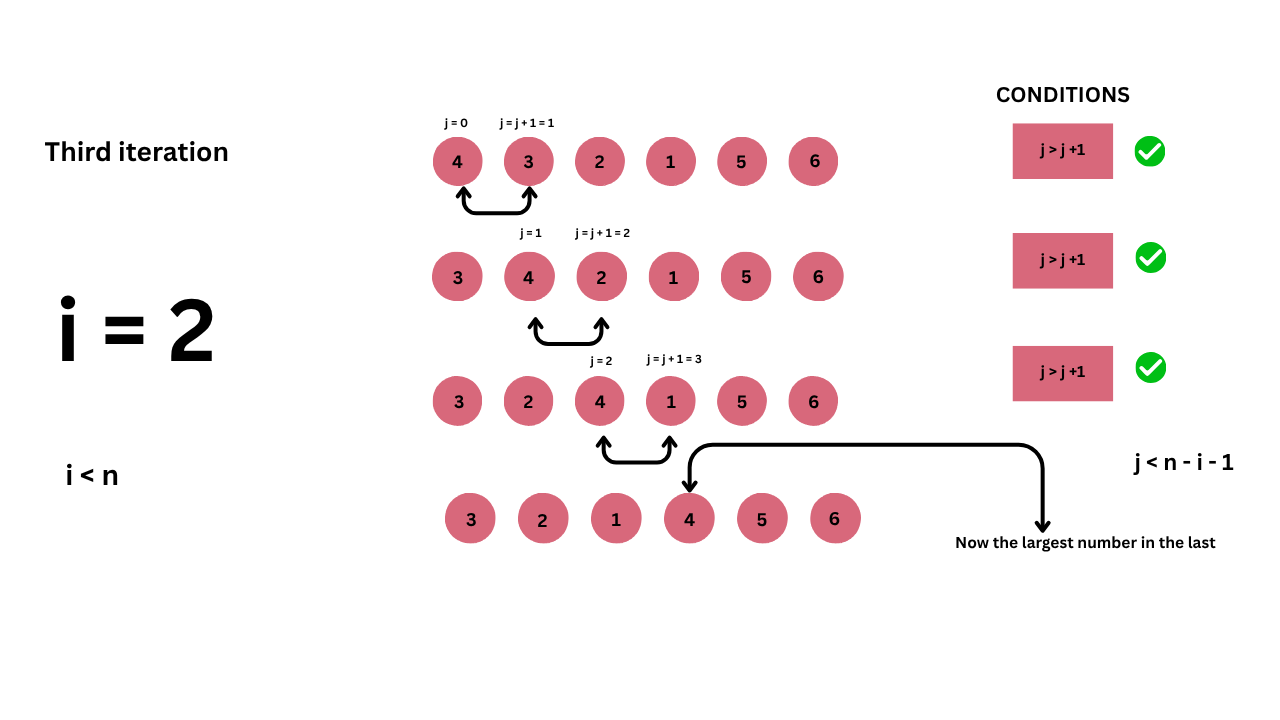
Next, in the third iteration:

1. Compare 4 and 3
   • Since 4 is greater than 3, swap the elements.
2. Compare 4 and 2
   • Since 4 is greater than 2, swap the elements.
3. Compare 4 and 1
   • Since 4 is greater than 1, swap the elements.

In the fourth iteration, we take the list {3, 2, 1, 4, 5, 6}, which is the result after the third iteration.

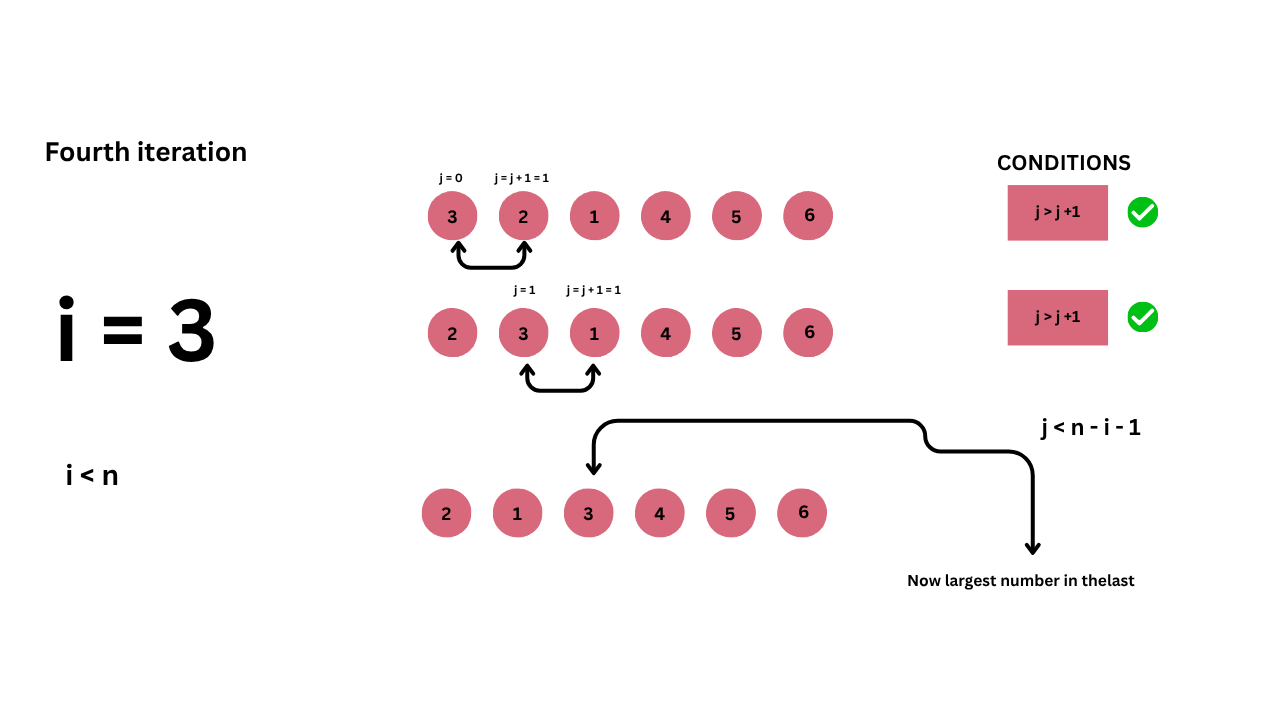
Next, we compare the elements again in the fourth iteration:

1. Compare 3 and 2
   • Since 3 is greater than 2, swap the elements.
2. Compare 3 and 1
   • Since 3 is greater than 1, swap the elements.

In the fifth iteration, we take the list {2, 1, 3, 4, 5, 6}, which is the result after the fourth iteration.

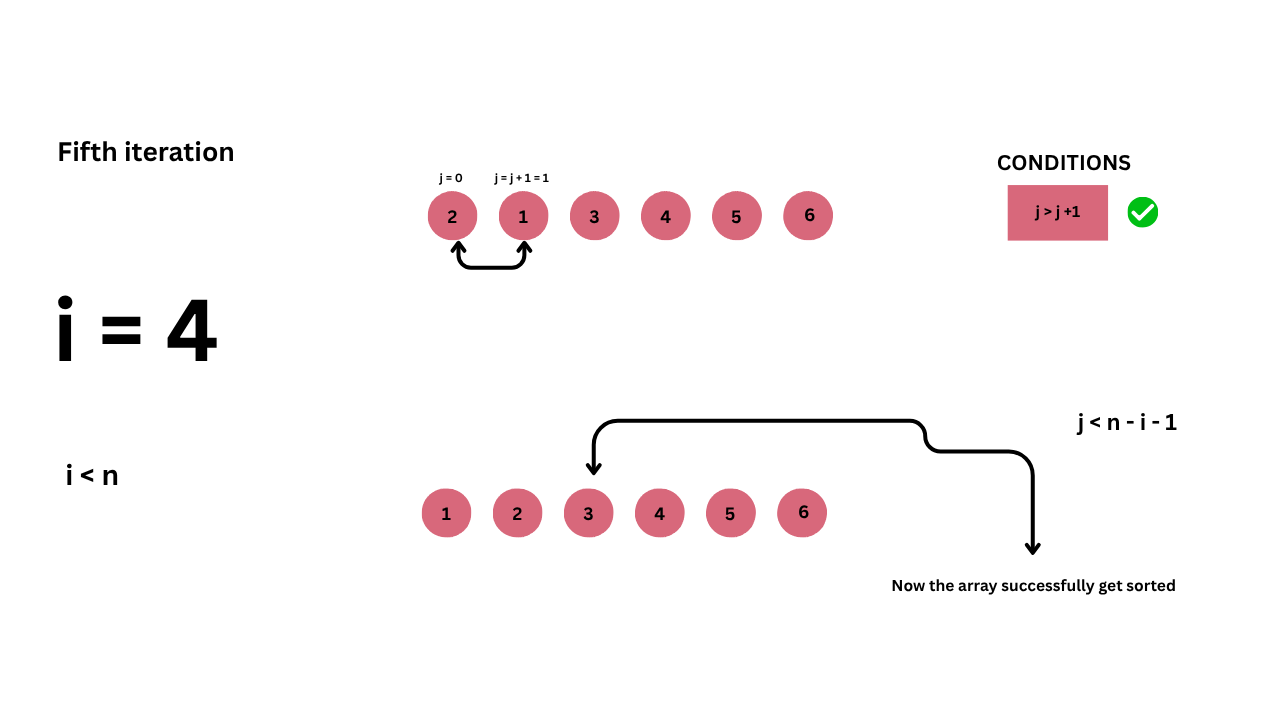
In the fifth iteration:

1. Compare 2 and 1
   • Since 2 is greater than 1, swap the elements.

Now your array has been successfully sorted.

After there is no swap, the loop gets terminated, and you get the sorted array or list.

Final Thoughts

So that’s how bubble sort works. I hope you now understand this algorithm better. In the next post, we’ll see how to implement it, analyze its performance, and explore ways to optimize the code.

I also hope this post didn’t just explain what bubble sort is, but also gave you a clearer idea of what an algorithm is and how to think about problem-solving. Remember, learning algorithms isn’t about memorizing steps or rushing to pass an interview.

It’s about building your problem-solving mindset and understanding how computers really work.

Enjoyed this guide? You can support me on Buy Me a Coffee — it helps me keep writing practical tutorials like this.

Thanks for reading and happy coding…………………………💻